Unified Koopman framework for robust data-driven identification of nonlinear systems
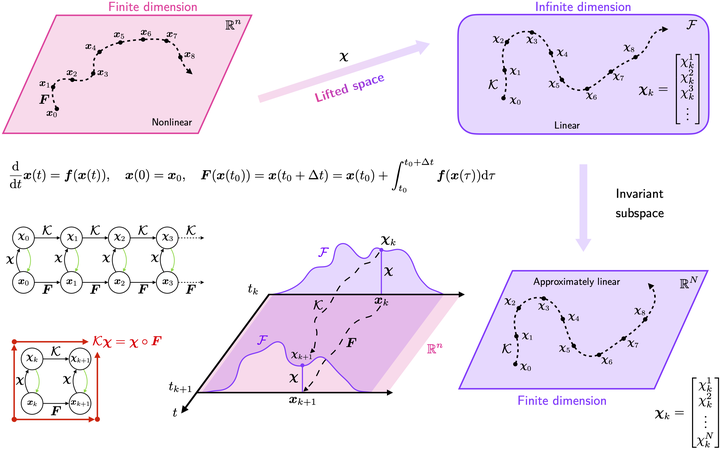 Image credit: Damien Guého
Image credit: Damien Guého
The objective of this research effort is to reconnect major subspace time-invariant and time-varying identification methods with the Koopman operator theoretic framework and offer a unified system identification structure for autonomous and non-autonomous systems. The concept of time-varying Koopman operator (TVKO) for accurate modeling of dynamical systems in a given domain around a reference trajectory is introduced. Subspace identification methods coupled with sparse approximation techniques deliver accurate models both in the continuous and discrete time domains. This allows for excellent reconstruction of several classes of nonlinear dynamical systems, from the chaotic behavior of the Lorenz oscillator to identifying the Newton’s law of gravitation. The connection between the Koopman operator and higher-order state transition matrices (STMs) is explicitly discussed. It is shown that subspace methods based on the Koopman operator are able to accurately identify the linear time varying model for the propagation of higher order STMs when polynomial basis are used as lifting functions.
Work in collaboration with Puneet Singla.